|
|
Research Topics
(current activities highlighted)

|
Synchronization of chaos
Phase synchronization
Synchronization in networks
Chimera states and other patterns of synchrony
Controlling synchrony
|
|

|
Inferring synchrony and coupling properties
Network reconstruction
Biomedical applications |
|

|
Strongly nonlinear lattices: First and second sound
Destruction of Anderson localization in nonlinear lattices
Lyapunov exponents in disordered systems
|
|

|
Phase compactons
Compactons vs chaos in lattices
Chaotic scattering
|
|

|
Coherence resonance
System-size resonance
Noise in systems with delay
Synchronization by common noise
Common noise and coupling
|
|

|
Lyapunov exponents and vectors
Globally coupled chaotic systems
Mixing flows |
|

|
Strange nonchaotic attractors
Singular continuous spectra
Renormalization group
Production systems
|
|

|
Simple systems with hyperbolic strange attractors
Attractors and repellers in reversible systems
Coupling sensitivity of chaos
|
|
Effects of noise
|
|
Effect of noise on a nonlinear dynamical system may be highly nontrivial. One often speaks on
noise-induced phenomena, when some features are observed solely due to presence of noise. In many cases a
dependence of some observed quantities on the noise amplitude is non-monotonic, these phenomena are called noise-induced
resonances.
|
|
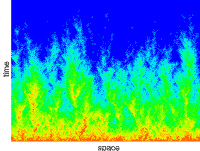
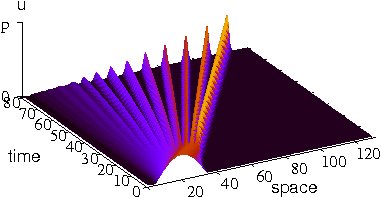
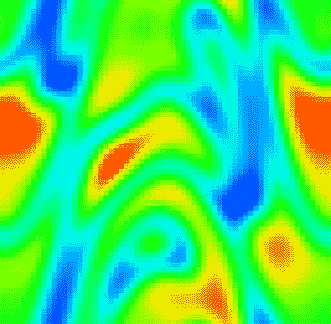
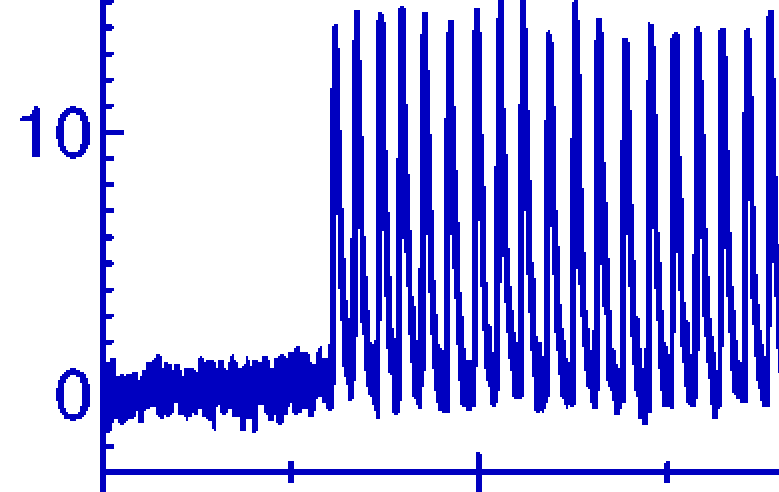
Coherence resonance is an effect of
maximal order of noise-induced oscillations at a certain noise level. It is usually observed
when the process has several characteristic time scales which differently depend on the noise level.
Most spectacular is coherence resonance in an excitable system (in the figure we depict the experiment of Miyakawa
and Isikawa with an excitable chemical reaction).
|
|
|
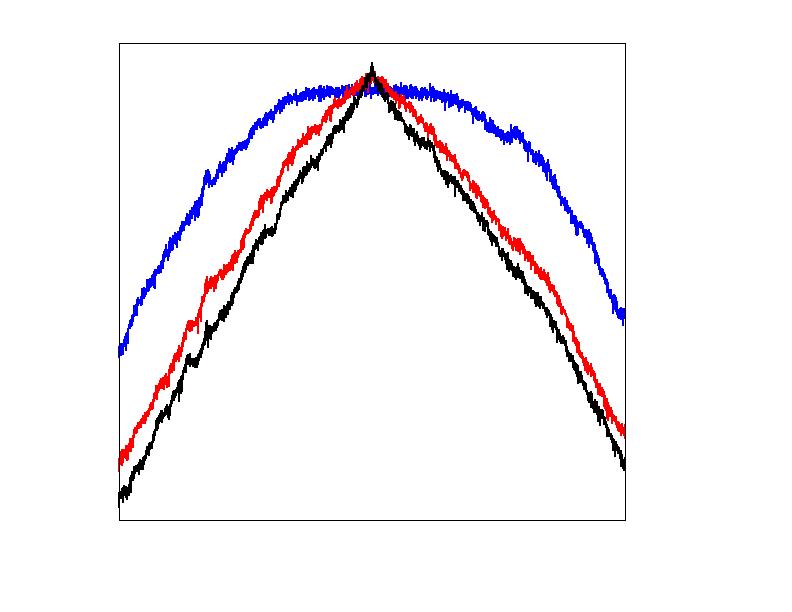
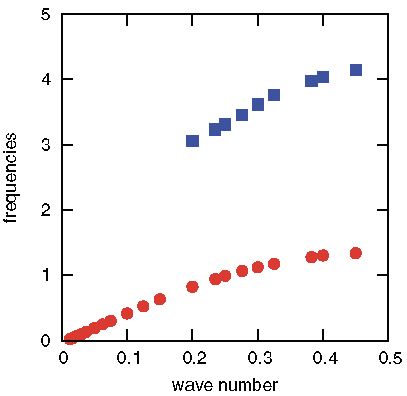
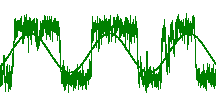
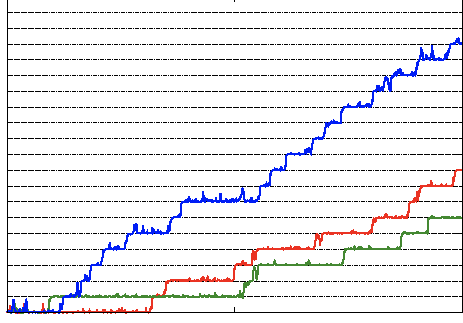
In ensembles of coupled noisy systems a phase transition to a collective
dynamics of the mean field may occur. In finite ensembles this dynamics is effectively
noisy due to finite-size effects. In such systems a resonance dependence on the noise level
appears as a system size resonance, when the maximal coherence or the maximal response to
an external force happens for a certain system size (figure). This effect occurs also for usual
phase transitions, e.g. for the Ising model.
|
|
|
|
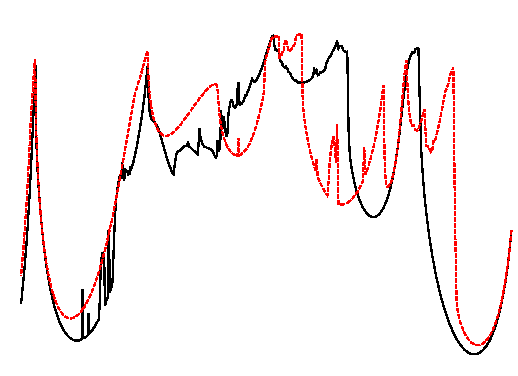
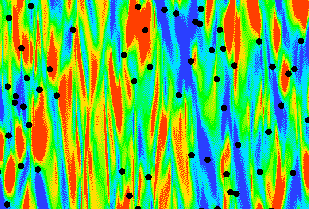
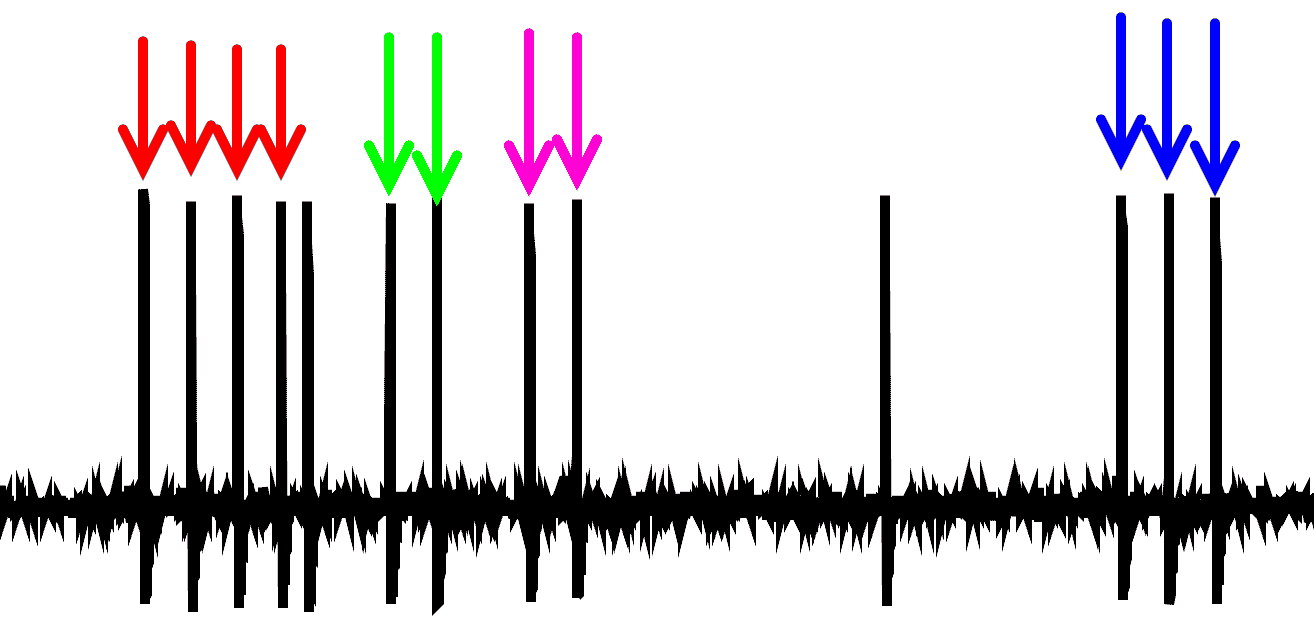
Many interesting effects appear when noise is acting on a system with
a delayed feedback. Because the noise-induced dynamics has its own, noise-dependent
time scale, nontrivial features can be observed when this time scale is close
to the delay time. In this way effects of delayed feedback on the noise-induced oscillations
in a bistable potential, in an excitable system (figure) has been considered.
|
|
|
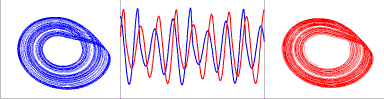
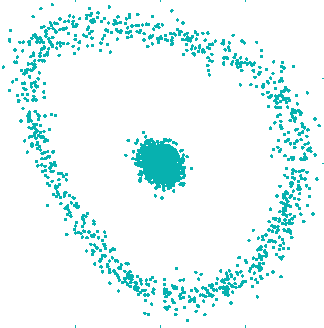
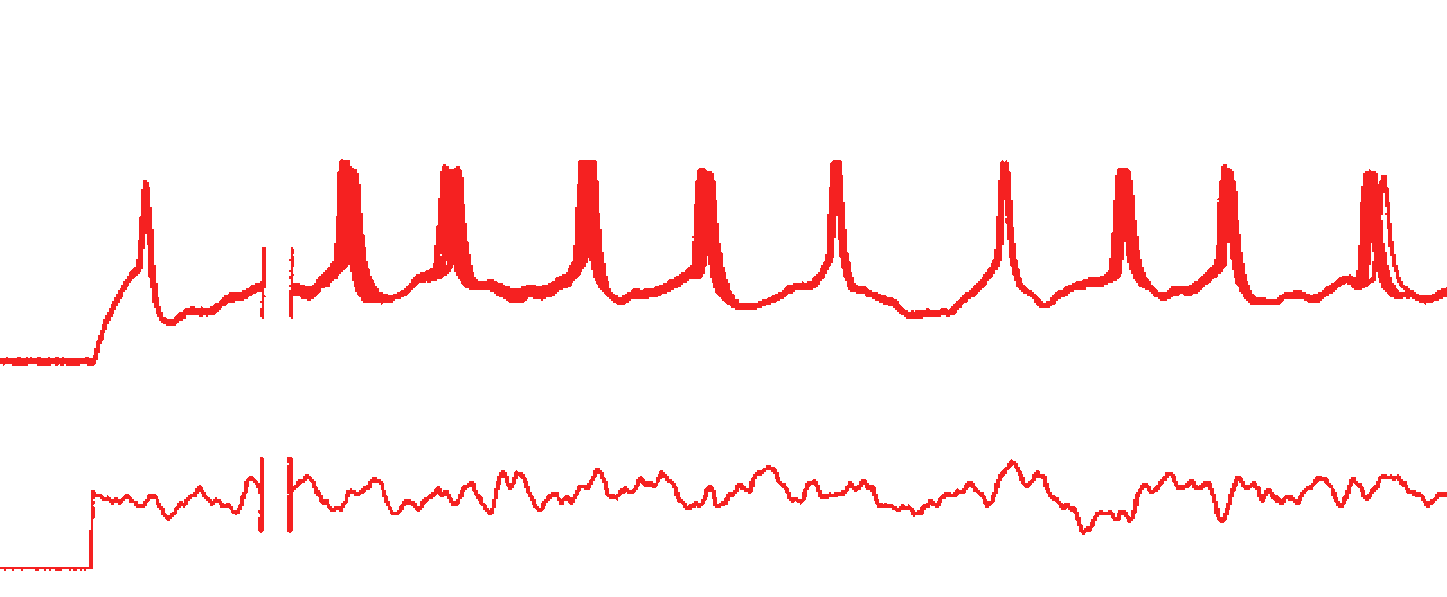
Noise can lead to synchronization of the systems. If two identical nonlinear systems are driven
with the same fluctuating force, their states can become identical. This effect is called
synchronization by common noise. It occurs when the Lyapunov exponent becomes negative, due to noise.
In neuroscience this phenomenon is known under name reliability of neuron spikes (figure shows
experiments by Hunter et al).
|
|
|
|
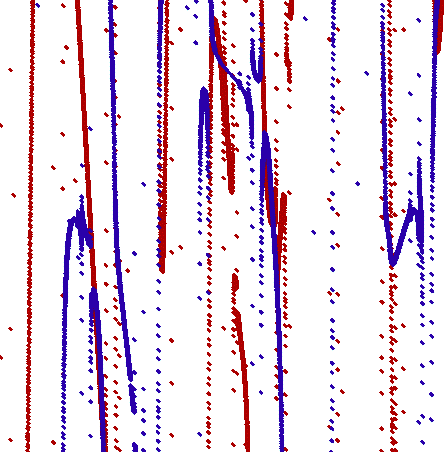
As a week common noise always synchronizes oscillators, nontrivial effects of coexistence of phase locking and
frequency anti-entrainment appear in ensembles of oscillators with repulsive coupling (figure).
|
|
|
|
Dynamics between order and chaos
|
|
Ordered (e.g. periodic and quasiperiodic) and chaotic behavior are well-established
objects of nonlinear dynamics. However, there is a large field of complex dynamics between order and
chaos. Probably, the best example of this is quantum chaos. However, also in classical systems
one accounts for complex dynamical states.
|
|
Strange nonchchaotic attractors can be observed in quasiperiodically forced systems.
They are non-chaotic because the Lyapunov exponent is negative, howevere they are fractals (figure).
Strange nonchaotic attractors appear, e.g., when a Josephson junction is driven with a two-frequency
force.
|
|
|
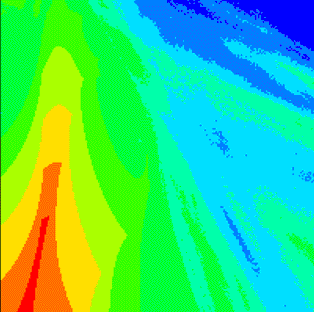
A power spectrum is a standard tool to study stationary processes. Usually one distinguishes
discrete and continuous spectra, these two types correspond to ordered and chaotic dynamics. However,
in between of these two major classes there are also singular continuous spectra. These fractal
spectra (see figure) have been studied, e.g., for strange nonchaotic attractors.
|

|
|
|
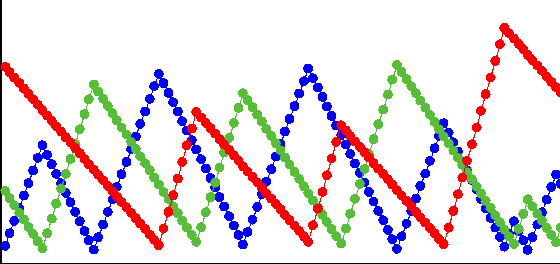
Renormalization group is a powerful method to study scaling behavior in dynamical systems.
It can be applied not only to transitions bewteen order and chaos, but also to the transitions between
strange nonchaotic, regular, and chaotic attractors (figure).
|
|
|
One of interesting applications of the behavior between chaos and order has appeared
in the modelling of production dynamics. Some models of deterministic queueing theory
give nonchaotic behavior with high complexity (figure). Production systems are nontrivial, because
they incorporate both discrete (symbolic) and continuous variables.
|
|
|
|
|
|