Reviews
...
the authors ... have pulled off a very difficult trick, that of
writing a book
that is both a definitive introduction to
synchronization
for the casual reader and a definitive text for
researchers
working
in a variety of fields.
William
Ditto,
Nature
...
has all the hallmarks of a classic. It is currently unique...
Every
scientist
working in the area will want a copy of this book,
and every
science librarian should buy one. No doubt it will run
through
many
editions, and deservedly.
Peter
McClintock,
Contemporary Physics
...
In an unconventional but excellent pedagogical choice, Arkady
Pikovsky, Michael
Rosenblum, and Jürgen Kurths begin by discussing
synchronization
without resorting to equations. It succeeds brilliantly.
Steven
Strogatz,
Physics Today
... The
book has a large text-and-figures-to-equations ratio, a feature
that greatly increases its usefulness for readers
new to the field. ...
The book includes bountiful examples, with real
data, from the life
sciences and the physical sciences.
"Synchronization" is most
suited,
I believe, for graduate students in the sciences,
engineering or
mathematics and other scientists who want to learn
about this exciting
and rapidly developing field.
Robert C. Hilborn,
Am. J. of Physics
Brief
contents
Part one: Synchronization without
formulae
Part two: Phase locking and frequency
entrainment
Part three: Synchronization of chaotic systems
Appendices:
Contents

- 1 Introduction
1.1 Synchronization in historical perspective
1.2 Synchronization: just a description
1.2.1 What is synchronization?
1.2.2 What is NOT synchronization?
1.3 Synchronization: an overview of different cases
1.3.1 Terminological remarks
1.4. Main bibliography


Part one: Synchronization without
formulae
- 2 Basic notions: self-sustained oscillator and its
phase
2.1 Self-sustained oscillators: mathematical models of natural systems
2.1.1 Self-sustained oscillations are typical in nature
2.1.2 Geometrical image of periodic self-sustained
oscillations:
limit cycle
2.2 Phase: definition and properties
2.2.1 Phase and amplitude of a quasilinear oscillator
2.2.2 Amplitude is stable, phase is free
2.2.3 General case: limit cycle of arbitrary shape
2.3 Self-sustained oscillator: main features
2.3.1 Dissipation, stability and nonlinearity
2.3.2 Autonomous and forced systems: phase of a forced system
is
not free!
2.4 Self-sustained oscillators: further examples and discussion
2.4.1 Typical self-sustained system: internal feedback loop
2.4.2 Relaxation oscillators


- 3 Synchronization of a periodic oscillator by external
force
3.1 Weakly forced quasilinear oscillator
3.1.1 The autonomous oscillator and the force in the rotating
reference
frame
3.1.2 Phase and frequency locking
3.1.3 Synchronization transition
3.1.4 An example: entrainment of respiration by mechanical
ventilator
3.2 Synchronization by external force: extended discussion
3.2.1 Stroboscopic observation
3.2.2 An example: periodically stimulated firefly
3.2.3 Entrainment by a pulse train
3.2.4 Synchronization of higher order. Arnold tongues
3.2.5 An example: periodic stimulation of atrial pacemaker
cells
3.2.6 Phase and frequency locking: general formulation
3.2.7 An example: synchronization of a laser
3.3 Synchronization of relaxation oscillators: special features
3.3.1 Resetting by external pulses. An example: cardiac
pacemaker
3.3.2 Electrical model of the heart by van der Pol and van der
Mark
3.3.3 Variation of the threshold. An example: electronic
relaxation
oscillator
3.3.4 Variation of the natural frequency
3.3.5 Modulation versus synchronization
3.3.6 An example: synchronization of the songs of snowy tree
crickets
3.4 Synchronization in the presence of noise
3.4.1 Phase diffusion in a noisy oscillator
3.4.2 Forced noisy oscillator. Phase slips
3.4.3 An example: entrainment of the respiration by mechanical
ventilation
3.4.4 An example: entrainment of the cardiac rhythm by weak
external
stimuli
3.5 Diverse examples
3.5.1 Circadian rhythms
3.5.2 Menstrual cycle
3.5.3 Entrainment of pulsatile insulin secretion by
oscillatory
glucose infusion
3.5.4 Synchronization in protoplasmic strands of Physarum
3.6 Phenomena around synchronization
3.6.1 Related effects at strong external forcing
3.6.2 Stimulation of excitable systems
3.6.3 Stochastic resonance from the synchronization viewpoint
3.6.4 Entrainment of several oscillators by a common drive


- 4 Synchronization of two and many oscillators
4.1 Mutual synchronization of self-sustained oscillators
4.1.1 Two interacting oscillators
4.1.2 An example: synchronization of triode generators
4.1.3 An example: respiratory and wing beat frequency of free
flying
barnacle geese
4.1.4 An example: transition between in-phase and anti-phase
motion
4.1.5 Concluding remarks and related effects
4.1.6 Relaxation oscillators. An example: true and latent
pacemaker
cells in the SA-node
4.1.7 Synchronization of noisy systems. An example: brain and
muscle
activity of a Parkinsonian patient
4.1.8 Synchronization of rotators. An example: Josephson
junctions
4.1.9 Several oscillators
4.2 Chains, lattices and oscillatory media
4.2.1 Synchronization in a lattice. An example: laser arrays
4.2.2 Formation of clusters. An example: electrical activity
of
a mammalian intestine
4.2.3 Clusters and beats in a medium: extended discussion
4.2.4 Periodically forced oscillatory medium. An example:
forced
Belousov-Zhabotinsky reaction
4.3 Globally coupled oscillators
4.3.1 Kuramoto self-synchronization transition
4.3.2 An example: synchronization of menstrual cycles
4.3.3 An example: synchronization of glycolytic oscillations
in
a population of yeast cells
4.3.4 Experimental study of rhythmic hand clapping
4.4 Diverse examples
4.4.1 Running and breathing in mammals
4.4.2 Synchronization of two salt-water oscillators
4.4.3 Entrainment of tubular pressure oscillations in nephrons
4.4.4 Populations of cells
4.4.5 Synchronization of predator--prey cycles
4.4.6 Synchronization in neuronal systems


- 5 Synchronization of chaotic systems
5.1 Chaotic oscillators
5.1.1 An exemplar: the Lorenz model
5.1.2 Sensitive dependence on initial conditions
5.2 Phase synchronization of chaotic oscillators
5.2.1 Phase and average frequency of a chaotic oscillator
5.2.2 Entrainment by a periodic force. An example: forced
chaotic
plasma discharge
5.3 Complete synchronization of chaotic oscillators
5.3.1 Complete synchronization of identical systems. An
example:
synchronization of two lasers
5.3.2 Synchronization of non-identical systems
5.3.3 Complete synchronization in a general context. An
example:
synchronization and clustering
of globally coupled electrochemical oscillators
5.3.4 Chaos-destroying synchronization


- 6 Detecting synchronization in experiments
6.1 Estimating phases and frequencies from data
6.1.1 Phase of a spike train. An example: electrocardiogram
6.1.2 Phase of a narrow-band signal. An example: respiration
6.1.3 Several practical remarks
6.2 Data analysis in ``active'' and ``passive'' experiments
6.2.1 ``Active'' experiment
6.2.2 ``Passive'' experiment
6.3 Analyzing relations between the phases
6.3.1 Straightforward analysis of the phase difference. An
example:
posture control in humans
6.3.2 High level of noise
6.3.3 Stroboscopic technique
6.3.4 Phase stroboscope in the case 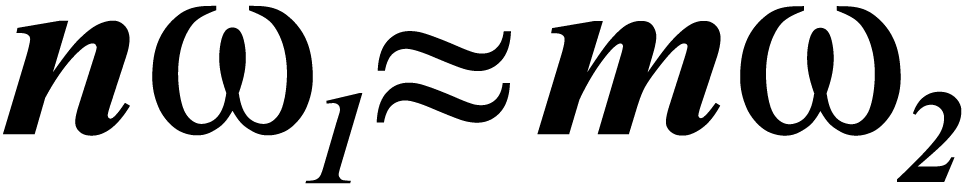 .
An example: cardiorespiratory interaction
.
An example: cardiorespiratory interaction
6.3.5 Phase relations in case of strong modulation. An
example:
spiking of electroreceptors of a paddlefish
6.4 Concluding remarks and bibliographic notes
6.4.1 Several remarks on ``passive'' experiments
6.4.2 Quantification and significance of the phase relation
analysis
6.4.3 Some related references


Part two: Phase locking and frequency
entrainment
- 7 Synchronization of periodic oscillators by
periodic external
action
7.1 Phase dynamics
7.1.1 A limit cycle and the phase of oscillations
7.1.2 Small perturbations and isochrones
7.1.3 An example: complex amplitude equation
7.1.4 The equation for the phase dynamics
7.1.5 An example: forced complex amplitude equations
7.1.6 Slow phase dynamics
7.1.7 Slow phase dynamics: phase locking and synchronization
region
7.1.8 Summary of the phase dynamics
7.2 Weakly nonlinear oscillator
7.2.1 The amplitude equation
7.2.2 Synchronization properties: isochronous case
7.2.3 Synchronization properties: nonisochronous case
7.3 Circle and annulus map
7.3.1 Circle map: derivation and examples
7.3.2 Circle map: properties
7.3.3 Annulus map
7.3.4 Large force and transition to chaos
7.4 Synchronization of rotators and Josephson junctions
7.4.1 Dynamics of rotators and Josephson junctions
7.4.2 Overdamped rotator in external field
7.5 Phase locked loops
7.6 Bibliographical notes


- 8 Mutual synchronization of two interacting
periodic
oscillators
8.1 Phase dynamics
8.1.1 Averaged equations for the phase
8.1.2 Circle map
8.2 Weakly nonlinear oscillators
8.2.1 General equations
8.2.2 Oscillation death, or quenching
8.2.3 Attractive and repulsive interaction
8.3 Relaxation oscillators
8.4 Bibliographic notes


- 9 Synchronization in the presence of noise
9.1 Self-sustained oscillator in the presence of noise
9.2 Synchronization in the presence of noise
9.2.1 Qualitative picture of the Langevin dynamics
9.2.2 Quantitative description for white noise
9.2.3 Synchronization by a quasiharmonic fluctuating force
9.2.4 Mutual synchronization of noisy oscillators
9.3 Bibliographic notes


- 10 Phase synchronization of chaotic systems
10.1 Phase of a chaotic oscillator
10.1.1 Notion of the phase
10.1.2 Phase dynamics of chaotic oscillators
10.2 Synchronization of chaotic oscillators
10.2.1 Phase synchronization by external force
10.2.2 Indirect characterization of synchronization
10.2.3 Synchronization in terms of unstable periodic orbits
10.2.4 Mutual synchronization of two coupled oscillators
10.3 Bibliographic notes


- 11 Synchronization in oscillatory media
11.1 Oscillator lattices
11.2 Spatially continuous phase profiles
11.2.1 Plane waves and targets
11.2.2 Effect of noise: roughening versus synchronization
11.3 Weakly nonlinear oscillatory medium
11.3.1 Complex Ginzburg-Landau equation
11.3.2 Forcing oscillatory media
11.4 Bibliographic notes


- 12 Populations of globally coupled oscillators
12.1 The Kuramoto transition
12.2 Noisy oscillators
12.3 Generalizations
12.3.1 Models based on phase approximation
12.3.2 Globally coupled weakly nonlinear oscillators
12.3.3 Coupled relaxation oscillators
12.3.4 Coupled Josephson junctions
12.3.5 Finite-size effects
12.3.6 Ensemble of chaotic oscillators
12.4 Bibliographic notes


Part three: Synchronization of chaotic systems
- 13 Complete synchronization I: Basic concepts
13.1 The simplest model: two coupled maps
13.2 Stability of the synchronous stat
13.3 Onset of synchronization: statistical theory
13.3.1 Perturbation is a random walk process
13.3.2 Statistics of finite-time Lyapunov exponents determines
diffusion
13.3.3 Modulational intermittency: power-law distributions
13.3.4 Modulational intermittency: correlation properties
13.4 Onset of synchronization: topological aspects
13.4.1 Transverse bifurcations of periodic orbits
13.4.2 Weak versus strong synchronization
13.4.3 Local and global riddling
13.5 Bibliographic notes


- 14 Complete synchronization II: Generalizations and complex
systems
14.1 Identical maps, general coupling operator
14.1.1 Unidirectional coupling
14.1.2 Asymmetric local coupling
14.1.3 Global (mean field) coupling
14.2 Continuous-time systems
14.3 Spatially distributed systems
14.3.1 Spatially homogeneous chaos
14.3.2 Transverse synchronization of space-time chaos
14.3.3 Synchronization of coupled cellular automata
14.4 Synchronization as a general symmetric state
14.4.1 Replica-symmetric systems
14.5 Bibliographic notes


- 15 Synchronization of complex dynamics by external forces
15.1 Synchronization by periodic forcing
15.2 Synchronization by noisy forcing
15.2.1 Noisy forced periodic oscillations
15.2.2 Synchronization of chaotic oscillations by noisy forcing
15.3 Synchronization of chaotic oscillations by chaotic forcing
15.3.1 Complete synchronization
15.3.2 Generalized synchronization
15.3.3 Generalized synchronization by quasiperiodic driving
15.4 Bibliographic notes


- Appendix 1 Discovery of synchronization by Christiaan Huygens
A1.1 A letter of Christiaan Huygens to Constantyn Huygens, father
A1.2 Sea clocks (sympathy of clocks). Part V
- Appendix 2 Instantaneous phase and frequency of a signal
A2.1 Analytic signal and the Hilbert Transform
A2.2 Examples
A2.3 Numerics: practical hints and know-hows
A2.4 Computation of the instantaneous frequency
Misprints
Please mail us if you found one!
- Page 94, line 1: (n+1)/n should be
n/(n-1)
- Page 192, last sentence in Sect. 7.2.1 should be:
We refer to these two situations as nonisochronous
and isochronous
cases, respectively. - Page 254,
line 13 after (10.8) should be:
Roughly speaking, D is proportional to the width...
- Page 280, Eq. 12.4: \omega_i should
be \omega_k
- Page 306, line -6 and page 307, line 1: log
should be ln
- Page 325, line 12: i-independent should
be k-independent
- Page 349, line 4: should
be
D_xy=min(2,1+\lambda_1/\lambda_y)
- Caption to Fig. 11.5: forced CGLE (11.1) should
be forced CGLE (11.19)
- Page 242, unnumbered equation for \lambda:
...=2\pi
Re(P_1) should be ...=2\pi
\epsilon Re(P_1)
- Page 204, line 6 in 1.: 2\pi(\eta-1)=2\pi(T-T_0)/T_0
should be \eta-2\pi=2\pi(T-T_0)/T_0
- Page 206, Eq. 7.56 should
be: \epsilon F_{min} \le
2\pi-\omega_0 t \le \epsilon F_{max}, and similarly for
Eq. 7.61
Contact
the authors
Mail to: Dept. of Physics and Astronomy, Potsdam University,
Karl-Liebknecht-Str. 24/25, 14476 Potsdam, Germany
E-mail to: pikovsky(appropriate
character)stat.physik.uni-potsdam.de
mros(appropriate character)uni-potsdam.de
juergen.kurths(appropriate character)pik-potsdam.de
Russian
edition
- Pycckoe u3gaHue
Last update 18.05.2014